Introduction
High quality research using fewer laboratory animals is a major challenge in many research areas. In 2006, the National Institute of Public Health and the Environment (RIVM) in the Netherlands launched the website www.interspeciesinfo.com to support researchers in reducing the use of laboratory animals. To provide a sustainable future for the website, it has been adopted by the 3Rs-Centre Utrecht Life Sciences (ULS) in 2015. The data in the Interspecies Database is managed by both RIVM and the 3Rs-Centre ULS. In the coming years the database will be expanded with more species, organs and parameters.
A user survey in 2010 has shown that information provided on the site has led to a significant reduction in the use of laboratory animals.
The website links you to a comprehensive database that provides freely available information on physiological, anatomical and biochemical parameters, such as organ weights, pH, CYP activities, GST, ventilation rates, and Escherichia coli counts. The content of the database mainly includes parameters in organs and tissues relevant for kinetics following oral exposure. Data are available on the same parameters for humans and various species of laboratory animals of different ages and strains. The information can be used for the development of a smart design of animal experiments in terms of choice of animal species, strain, sex and age that is most relevant for humans with regard to the relevant exposure scenario.
Stay updated
In case you want to stay informed about the content and updates of the Interspecies Database, please send an e-mail to 3RsCentreULS@uu.nl.
Background
Numerous studies in which a variety of compounds were tested have demonstrated that interspecies differences can be substantial, hampering reliable extrapolation of the results to the human situation. There are of course many differences between animal species themselves as well as between animals and man. These differences may influence the kinetics and/or dynamics of a compound, e.g. long nose (inhalatory exposure), fur (topical application), intestinal anatomy and physiology, differences in metabolic pathways, metabolic rates, extent of biliary excretion, etc. There are, on the other hand, also various similarities between animals and humans, e.g. liver as important metabolising organ, liver and kidney as important excretory organs, comparable circulatory systems and specialised mechanisms for the elimination of xenobiotics.
This website can help to gain insight into the impact of anatomical and physiological (including biotransformation) differences between species and within species on the kinetics of xenobiotics. The information can be used for the development of a smart design of animal experiments in terms of choice of animal species, strain, sex and age and subsequently to improved animal human extrapolation.
Meta-analysis of data from multiple sources
The purpose of the meta-analysis is to summarise the reported data for a given parameter by a single mean value, together with a measure of the associated uncertainty in that value. The uncertainty will be smaller (larger) when the number of available studies reporting a particular parameter is larger (smaller), and when the variation among studies is smaller (larger). If reported, the sample sizes (N) as used in the various studies are taken into account, by giving studies with a larger N more weight in calculating the overall mean value over studies. In particular,
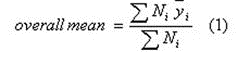
where i denotes the arithmetic or geometric (see below) mean of study i, and Ni the sample size for that study.
A practical problem is that most studies report arithmetic means, while others report geometric means. The geometric mean is a preferable mean value for representing the ‘typical’ value of a kinetic parameter, and therefore a reported arithmetic mean (AM) is translated into a geometric mean (GM), if possible, which is the case if the studies report the standard deviations (SD) as well. This is done by first calculating the coefficient of variation (CV):
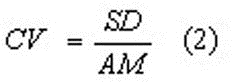
and then the geometric mean (GM) by:
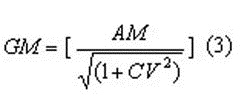
The underlying assumption is that the individual observations (within a study) are log normally distributed.
The uncertainty in the overall mean obtained by expression (1) is expressed as a factor, indicating by how much the “true” value could be lower or higher. This factor is calculated by first calculating the confidence interval for the overall study mean, on log-scale, in the usual way, i.e., divide the standard deviation among studies by the square root of the number of studies, and multiply that value by student’s t for deriving the lower bound of the confidence interval (at one-sided 95%-confidence level). Back-transforming the difference between the overall mean and the just derived lower confidence bound (both on log-scale) results in the factor expressing the uncertainty in the overall mean.
